Задачи

Для треннировки и проверки своих знаний

Задача

Задача — проблемная ситуация с явно заданной целью, которую необходимо достичь; в более узком смысле задачей также называют саму эту цель, данную в рамках проблемной ситуации, т. е. то, что требуется сделать.

Решение задач

Решение задач — процесс, являющийся составной частью мышления; выполнение действий или мыслительных операций, направленное на достижение цели, заданной в рамках проблемной ситуации. С точки зрения когнитивного подхода процесс решения задач является наиболее сложной из всех функций интеллекта и определяется как когнитивный процесс более высокого порядка, требующий согласования и управления более элементарными или фундаментальными навыками.

Задачей можно назвать, например, ситуацию, когда нужно достать предмет, находящийся очень высоко; второе значение слышится в указании: «Ваша задача — достать этот предмет». Несколько более жёсткое понимание «задачи» предполагает явными и определёнными не только цель, но и условия задачи, которая в этом случае определяется как осознанная проблемная ситуация с выделенными условиями (данным) и требованием (целью). Ещё более узкое определение называет задачей ситуацию с известным начальным состоянием системы и конечным состоянием системы, причём алгоритм достижения конечного состояния от начального известен (в отличие от проблемы, в случае которой алгоритм достижения конечного состояния системы не известен).

В более широком смысле под задачей также понимается то, что нужно выполнить — всякое задание, поручение, дело, — даже при отсутствии каких бы то ни было затруднений или препятствий в выполнении. В учебной и т. п. практике «задача», напротив, принимает более узкий смысл и обозначает упражнение, требующее нахождения решения по известным данным с помощью определённых действий (умозаключения, вычисления, перемещения элементов и т. п.) при соблюдении определённых правил совершения этих действий (логическая задача, математическая задача, шахматная задача).

Кинематика

Равномерное прямолинейное движение

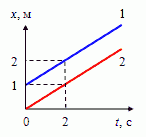На рисунке представлены графики зависимости координаты двух тел от времени. Графики каких зависимостей показаны? Какой вид имеют графики зависимости скорости и пути пройденного телом, от времени?

Решение:

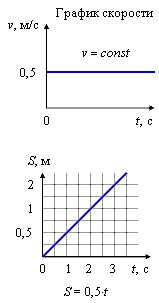На рисунке показаны графики равномерного движения тел.

1) В начальный момент времени t = 0 первое тело имеет начальную координату хо1 = 1 м, второе тело — координату хо2 = 0.

2) Оба тела движутся в направлении оси Х, так как координата возрастает с течением времени.

3) Уравнение движения для равномерного прямолинейного движения имеет вид: x=xо+vхt.

Тогда для первого, второго тела соответственно: x1=xо1+v1хt и x2=xо2+v2хt или x1=1+v1хt, x2=v2хt.

Определим скорости первого и второго тела: v1x = x1 - 1/ t = 2- 1/2 = 0,5 м/с.

v2x/ t = x2/2 = 1 = 0,5 м/с.

Уравнения скорости имеют вид: v1х=v2х=0,5 м/с.

Так как S=vхt, то уравнение пути S=0,5t.

Равноускоренное и равнозамедленное движение

Наблюдатель, стоящий на платформе, определил, что первый вагон электропоезда прошёл мимо него в течение 4 с, а второй — в течение 5 с. После этого передний край поезда остановился на расстоянии 75 м от наблюдателя. Считая движение поезда равнозамедленным, определить его начальную скорость, ускорение и время замедленного движения.

Решение:

Составим уравнение движения для первого вагона: L = vot1 - at1^2/ 2,

для двух вагонов сразу: 2L = vo(t1 + t2) - a(t1 + t2)^2/2 .

Нам понадобится еще одно уравнение, в котором будет скорость и ускорение: S = vo^2/2a .

Таким образом, мы имеем систему из трех уравнений, решая которую (поупражняйтесь в математике самостоятельно), выйдем на конечную формулу:

a = 8S(t2 - t1)^2 /(2t1t2 + t2^2 - t1^2)^2 = 0.25 м/с2

Свободное падение

Тело, брошенное вертикально вниз с начальной скоростью 5 м/с, в последние 2 с падения прошло путь вдвое больший, чем в две предыдущие 2 с. Определить время падения и высоту, с которой тело было брошено. Построить график зависимости пройденного пути, ускорения и скорости от времени.

Решение:

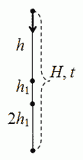
Сделаем рисунок к задаче и введем следующие обозначения:

h1 — расстояние пройденное телом в две предыдущие секунды, тогда
2h1 — расстояние пройденное телом за последние две секунды,
t — время падения с высоты H.

Высота падения тела H равна: H = vot + gt^2/ 2 (1),

а высота h (без четырех секунд) равна: h = vo(t - 4) + g(t - 4)^2 /2 (2).

Вычитая из уравнения (1) уравнение (2), получим: 3h1 = 4vo + gt2/2 - g(t - 4)^2/ 2

То есть: h1 = 4/3 vo + gt^2/6 - g(t - 4)^2/6 (3).

Составим еще одно уравнение высоты: h + h1 = vo(t - 2) + g(t - 2)^2/2 (4).

Вычитая из уравнения (1) уравнение высоты (4), получим в конце:
h1 = vo + gt^2/4 - g(t - 2)^2/4 (5).

Приравнивая правые части уравнений (3) и (5), имеем (после преобразований) t = 4,5 c, тогда высоту, с которой падало тело, можно рассчитать по формуле (1). Высота равна 123,75 м.

Для построения графиков составим уравнения пути H(t), g(t) и v(t):

H = 5t +5t^2, g = 10 м/с^2 = const, v = 5 + 10t.

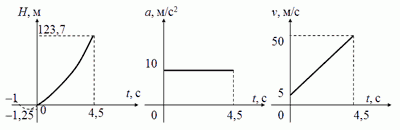
Примечание: начало отсчета выбиралось в точке бросания тела, и ось направлялась вертикально вниз (по вектору начальной скорости и ускорения), что видно из графиков.

Криволинейное движение

Если камень, брошенный под углом 30° к горизонту, находился в полете 2 с, то с какой скоростью он упал на землю?

Решение:

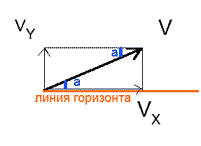
Если камень был в полете 2 с, то в силу симметрии 1 с он летел до максимальной точки подъема и 1 с падал вниз (сопротивлением воздуха мы пренебрегаем). В максимальной точке подъема камень имеет только горизонтальную составляющую Vx скорости V. Свободно падая с максимальной высоты подъема, за 1 с камень приобретет вертикальную скорость Vy, равную:

Vy = gt

Скорость бросания равна скорости падения тела, которая связана с вертикальной составляющей в момент падения:

V = vy/sin a = gt/sin a

Искомая скорость равна V = 20 м/с.

Движение по окружности

На краю горизонтальной платформы стоит человек массой 80 кг. Платформа представляет собой круглый однородный диск массой 160 кг, вращающийся вокруг вертикальной оси, проходящий через ее центр, с частотой 6 об/мин. Сколько оборотов в минуту будет делать платформа, если человек перейдет от края платформы к ее центру? Момент инерции рассчитывать как для материальной точки.

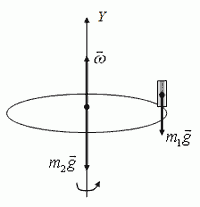
Система «человек–платформа» замкнута в проекции на ось Y, т. к. моменты сил Mm1g = 0 и Mm2g = 0 на эту ось. Следовательно, можно воспользоваться законом сохранения момента импульса. В проекции на ось Y:

J1w1 = J2w2, (1)

где J1 — момент инерции платформы с человеком, стоящим на ее краю, J2 — момент инерции платформы с человеком, стоящим в центре, w1 и w2 — угловые скорости платформы в обоих случаях.

Здесь J1 = m2R^2/2 + m1R^2,

J2 = m2R^2/2 , (2)

где m1, m2 — массы человека и платформы соответственно, R — радиус платформы.

Подставляя (2) в (1) и учитывая, что w = 2?n, где n — частота вращения платформы, получим:

(m2R^2/2 + m1R^2)*2пn1 = m2R^2/2*2пn2

Решаем последнее уравнение относительно неизвестной частоты вращения "платформы-человек" n2:

n2 = m2 + 2m1/m2 *n1.

После вычислений: n2 = 0.2 (об/с) = 12 об/мин.