Задачи
Для треннировки и проверки своих знаний
Задача

Задача — проблемная ситуация с явно заданной целью, которую необходимо достичь; в более узком смысле задачей также называют саму эту цель, данную в рамках проблемной ситуации, т. е. то, что требуется сделать.
Решение задач
Решение задач — процесс, являющийся составной частью мышления; выполнение действий или мыслительных операций, направленное на достижение цели, заданной в рамках проблемной ситуации. С точки зрения когнитивного подхода процесс решения задач является наиболее сложной из всех функций интеллекта и определяется как когнитивный процесс более высокого порядка, требующий согласования и управления более элементарными или фундаментальными навыками.



Задачей можно назвать, например, ситуацию, когда нужно достать предмет, находящийся очень высоко; второе значение слышится в указании: «Ваша задача — достать этот предмет». Несколько более жёсткое понимание «задачи» предполагает явными и определёнными не только цель, но и условия задачи, которая в этом случае определяется как осознанная проблемная ситуация с выделенными условиями (данным) и требованием (целью). Ещё более узкое определение называет задачей ситуацию с известным начальным состоянием системы и конечным состоянием системы, причём алгоритм достижения конечного состояния от начального известен (в отличие от проблемы, в случае которой алгоритм достижения конечного состояния системы не известен).
В более широком смысле под задачей также понимается то, что нужно выполнить — всякое задание, поручение, дело, — даже при отсутствии каких бы то ни было затруднений или препятствий в выполнении. В учебной и т. п. практике «задача», напротив, принимает более узкий смысл и обозначает упражнение, требующее нахождения решения по известным данным с помощью определённых действий (умозаключения, вычисления, перемещения элементов и т. п.) при соблюдении определённых правил совершения этих действий (логическая задача, математическая задача, шахматная задача).
Законы сохранения
Закон сохранения энергии
Молоток массой 0,80 кг в момент удара о шляпку гвоздя имеет скорость 1,5 м/с и забивает его в бревно на глубину 5,0 мм. Какой массы груз необходимо положить на шляпку гвоздя, чтобы он вошел в бревно на такую же глубину?
На горизонтальной плоскости находятся две тонкостенные трубы радиуса R каждая, оси которых параллельны. Вначале одна из труб, имеющая массу m, покоится, а вторая, имеющая массу 2m, катится без проскальзывания по направлению к первой со скоростью поступательного движения v. Считая столкновение труб абсолютно упругим, найдите зависимость от времени скоростей поступательного и вращательного движений второй трубы. Нарисуйте графики этих зависимостей. Коэффициент трения скольжения труб о горизонтальную поверхность равен k. Трением между трубами при столкновении пренебречь. Какая часть кинетической энергии, оставшейся у второй трубы после удара, перешла в тепло при её последующем движении? Так как трение между трубами пренебрежимо мало, то можно считать, что при соударении труб вращение одной из них не передается второй. Поэтому, рассматривая соударение труб, мы можем не учитывать вращение первой (первоначально движущейся) трубы.
Задачи развивающие нестандартное мышление Задачи по кинематике с решениями Задачи по электростатике с решениями Задача по постоянному току с решением Задачи с решениями по магнетизму и магнитным явлениям. Задачи с решениями по молекулярно-кинетической теории, термодинамике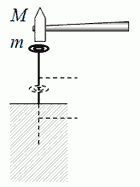 Рассмотрим начальные условия (см. рисунок слева).
Рассмотрим начальные условия (см. рисунок слева).
Молоток имеет кинетическую энергию в момент удара mv^2/2, потенциальную энергию Mgh (начальный уровень связан с положением шляпки гвоздя после удара). Для упрощения возьмем массу гвоздя сосредоточенной в шляпке. Гвоздь имеет потенциальную энергию mgh. Здесь h = 5,0 мм — глубина погружения гвоздя после удара молотком.
После удара: потенциальная энергия гвоздя равна нулю, кинетическая энергия молотка равна нулю, потенциальная энергия молотка равна нулю. Энергия, затраченная на работу против сил сопротивления движению гвоздя в бревне, равна
Из закона сохранения энергии:
Mv^2/2 + Mgh + mgh =
Рассмотрим вторую ситуацию. Необходимо положить груз массы M1 так, чтобы гвоздь опустился на такую же глубину.
Начальные условия: потенциальная энергия груза M1gh, потенциальная энергия гвоздя mgh. В конечном положении потенциальные энергии груза и гвоздя равны нулю, так как нулевой уровень связан с конечным положением шляпки. Энергия, затраченная на работу против сил сопротивления движению гвоздя в бревне, также равна
Тогда:M1gh + mgh =
Приравняем правые части уравнений (1) и (2):
Mv^2 /2 + Mgh + mgh = M1gh + mgh.
M1 = Mv^2/2gh + M.
При M = 0,8 кг, v = 1,5 м/с, h = 5 мм, после вычислений имеем M1 = 18.8 кг.
Задача №2
Запишем для столкновения труб законы сохранения энергии и импульса:
mvo = mv1 + mv2.
mvo^2/2 = mv1^2/2 + mv2^2/2 ,
где v1 и v2 — скорости поступательного движения соответственно первой и второй труб после соударения.
Решая эти уравнения совместно, найдем, что v1 = 0 и v2 = vo, то есть при соударении трубы обмениваются скоростями поступательного движения — точно так же, как при соударении двух одинаковых шаров.
Рассмотрим теперь, что будет происходить с первой, первоначально двигавшейся трубой после удара. В системе координат, связанной с осью трубы, катящейся без проскальзывания по плоскости со скоростью vo. Это означает, что такая труба вращается вокруг своей оси так, что линейная скорость вращения точек ее поверхности равна по величине скорости поступательного движения оси трубы. Поэтому первая труба после столкновения вращается вокруг своей оси с угловой скоростью w = vo/R.
Сила трения Fтр = kmg, действующая на эту трубу, замедляет ее вращение и одновременно сообщает ей ускорение:
a = Fтр /m = kg.
в направлении первоначального движения трубы. К моменту t эта труба будет иметь скорость поступательного движения:
u1' = at = kgt
и будет вращаться вокруг своей оси с угловой скоростью:
w1 = vo - kgt/R .
Скорость поступательного движения трубы увеличивается, а скорость вращения трубы уменьшается пропорционально времени. К моменту to, когда скорость поступательного движения оси трубы станет равна линейной скорости вращения трубы вокруг оси, проскальзывание трубы относительно плоскости прекратится, и после этого ни скорость вращения трубы w1', ни скорость поступательного движения оси трубы u1' уже не будут меняться.
Из условия
kgto = vo - kgto
найдем, что
to = vo / 2kg .
В этот момент
u1 = vo/2 и w1 = vo/2 .
Рассматривая аналогично движение второй трубы, найдем, что действующая на нее сила трения уменьшает скорость ее поступательного движения: u1 = vo ? kgt
и увеличивает угловую скорость вращения:
w2 = kgt/R .
К моменту t = vo/2kg проскальзывание трубы относительно плоскости прекратится. В этот момент труба будет иметь не меняющиеся в дальнейшем скорость поступательного движения u2 = vo/2 и угловую скорость вращения вокруг оси w2 = vo/2R.
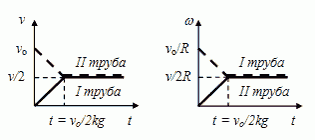 Графики зависимости скоростей поступательного движения труб и их угловых скоростей вращения от времени показаны на рисунке слева.
Графики зависимости скоростей поступательного движения труб и их угловых скоростей вращения от времени показаны на рисунке слева.
Задачи
Логические задачи
Кинематика
Электростатика
Постоянный ток
Магнетизм
МКТ, термодинамика